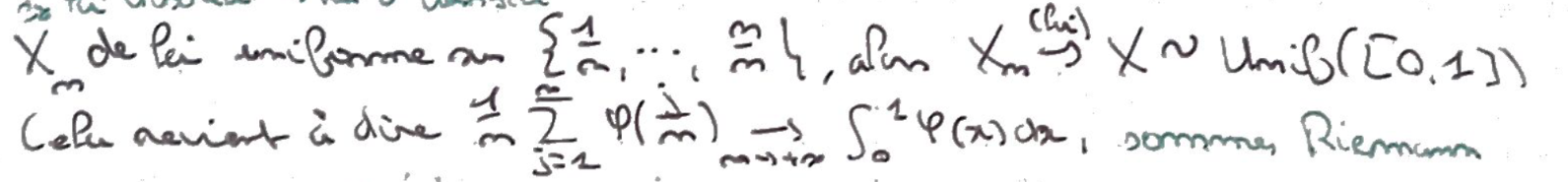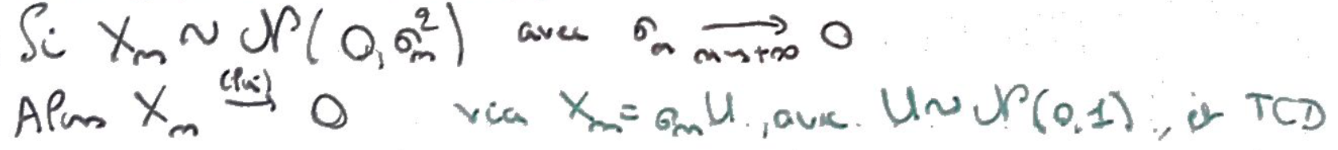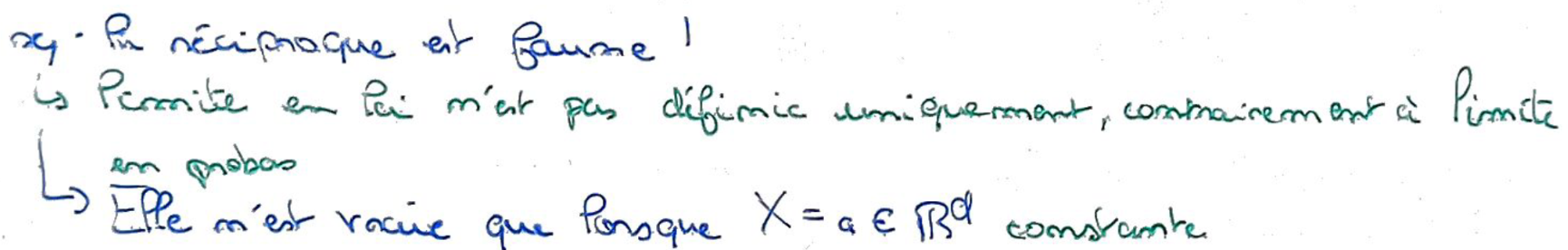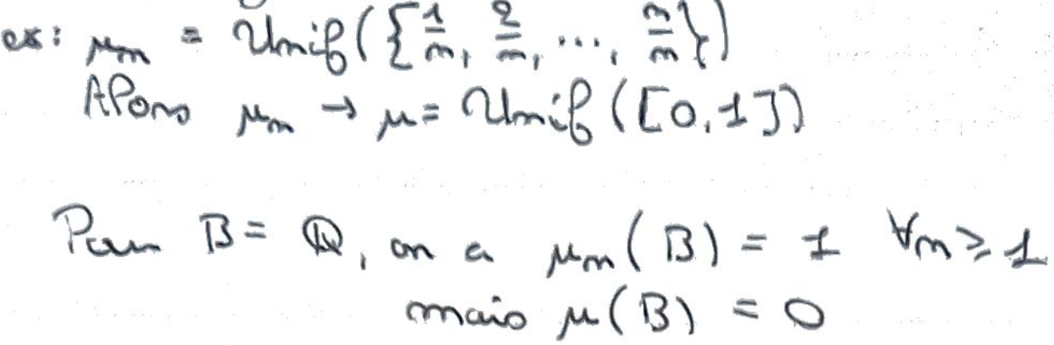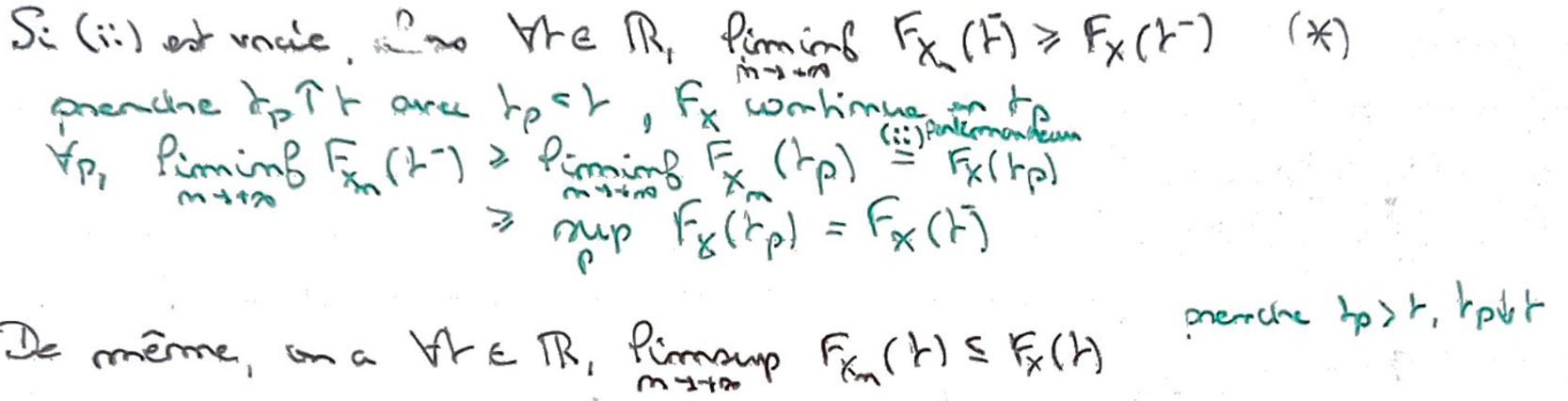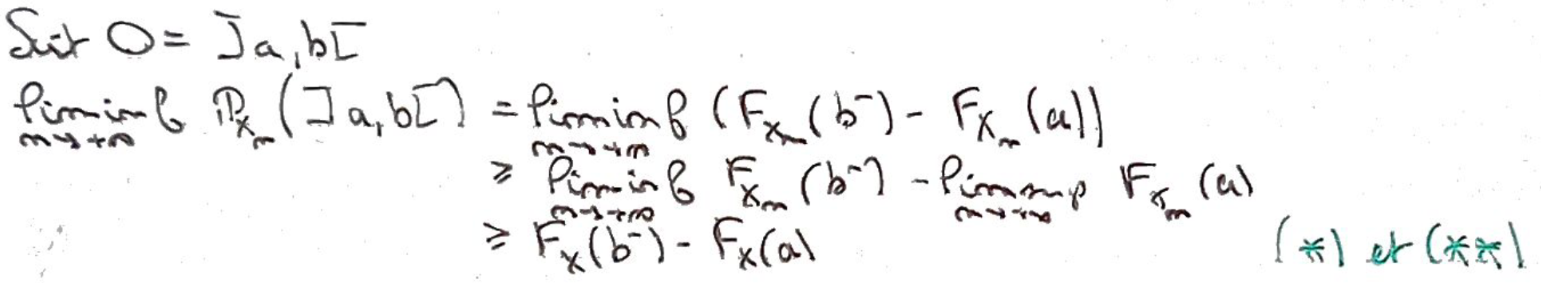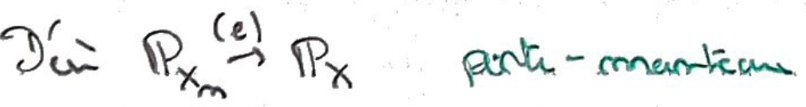Math'φsics

Menu
  • Acceuil
  • Maths
  • Physique
    • Maths
    • Physique
  • Convergence en loi

    Formulaire de report


    Convergence en loi \(X_n\overset{(\text{loi})}\longrightarrow X\)
    On a la Convergence étroite des Lois \({\Bbb P}_{X_n}\) vers \({\Bbb P}_X\). $$\forall \varphi\in\mathcal C_b({\Bbb R}^d),\quad{\Bbb E}[\varphi(X_n)]{\underset{n\to+\infty}\longrightarrow}{\Bbb E}[\varphi(X)]$$
    • caractérisation dans le cas discret : \(\forall x,{\Bbb P}(X_n=x){\underset{n\to+\infty}\longrightarrow}{\Bbb P}(X=x)\)
    • dans le cas continu, \(p_n(x)\overset{pp}{\underset{n\to+\infty}\longrightarrow} p(x)\) entraîne la convergence en loi
    • la convergence en loi est entraînée par tous les autres modes de convergence
      •     
    • si \(X=a\in{\Bbb R}^d\) est une constante, alors la convergence en loi entraîne la converge en probabilité
    • caractérisations (dans le cas continu) :
            
      1. Via le Théorème du porte-manteau

        
  • On a la convergence ponctuelle des Fonction de répartitions : \(F_{X_n}(t){\underset{n\to+\infty}\longrightarrow} F_X(t)\), pour tout \(t\in{\Bbb R}\) où \(F_X\) est continue
    •     
  • (théorème de Lévy) : on a la convergence ponctuelle des Fonction caractéristiques : \(\forall \xi\in{\Bbb R}^d,\Phi_{X_n}(\xi){\underset{n\to+\infty}\longrightarrow}\Phi_X(\xi)\)


    • Questions de cours

    Démontrer :

    On prend \(\varphi\) à valeurs dans \([0,1]\).

    Le Lemme de Fatou nous donne une inégalité.

    Rappliquer le Lemme de Fatou à \(1-\varphi\) donne la seconde inégalité.


    START
    Ω Basique (+inversé optionnel)
    Recto: Donner un exemple de famille de v.a. Discrètes qui converge en loi vers une v.a. À densité.
    Verso:

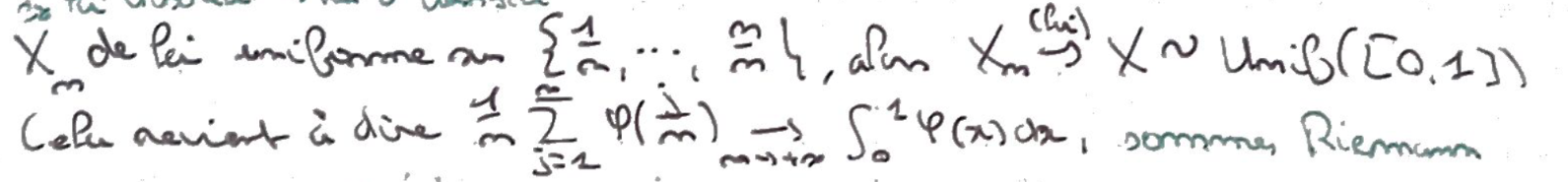
    Bonus: Sommes de Riemann Carte inversée ?:
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Donner un exemple de famille de v.a. À densité qui converge en loi vers une v.a. Discrète.
    Verso:

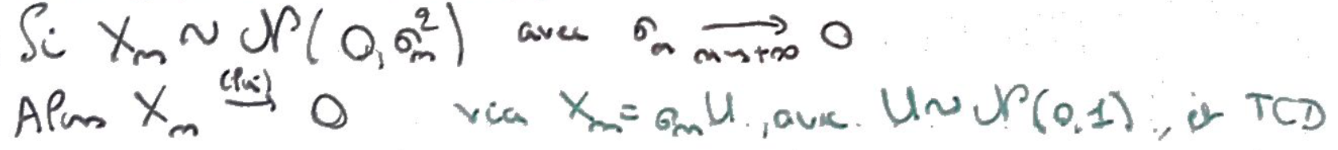
    Bonus:
    Carte inversée ?:
    END
    Démontrer :

    On suppose dans un premier temps qu'on a la convergence presque sûre.

    Alors on a la convergence de l'image par \(\varphi\in\mathcal C_b({\Bbb R}^d)\), et donc par TCD la convergence en loi.

    Dans le cas général, on a une sous-suite qui converge ps, et donc on a la convergence en loi le long d'une sous-suite.

    Ce résultat est valable pour toute sous-suite de \((X_n)_n\).

    Toutes les sous-suites admettent une sous-suite qui converge en loi, ce qui nous donne la convergence en loi pour toute la suite.


    START
    Ω Basique (+inversé optionnel)
    Recto: Expliquer pourquoi dans le cas général, la convergence en loi n'entraîne pas la convergence en probabilité.
    Verso:

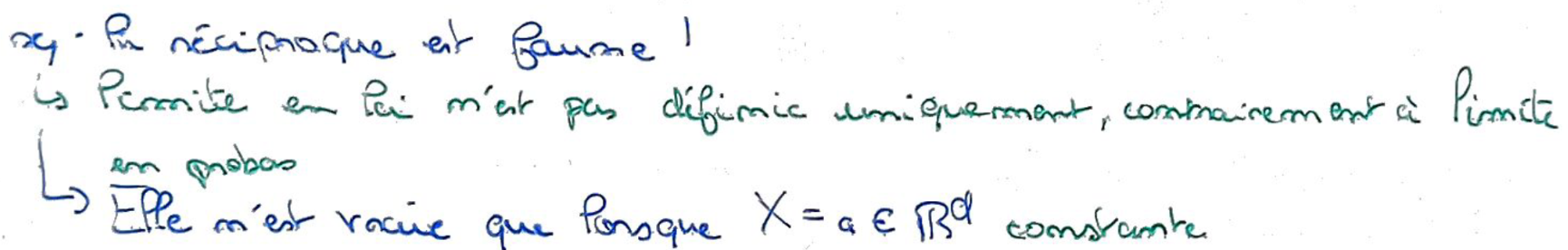
    Bonus:
    Carte inversée ?:
    END
    START
    Ω Basique (+inversé optionnel)
    Recto:

    Donner un contre-exemple.
    Verso:

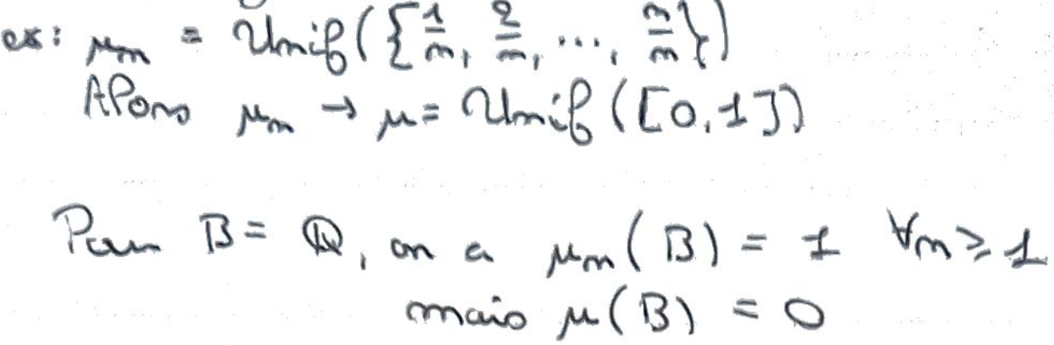
    Bonus:
    Carte inversée ?:
    END
    Démontrer \((i)\implies(ii)\) :

    Si \(F_X\) est continue en \(t\), alors on a \({\Bbb P}_X(\{t\})=0\).

    Or \(\{t\}\) est la Frontière de \(]-\infty,t]\), ce qui fait qu'on a le résultat par Théorème du porte-manteau.


    Exo-Démo
    Démontrer \((ii)\implies(i)\) :

    1:

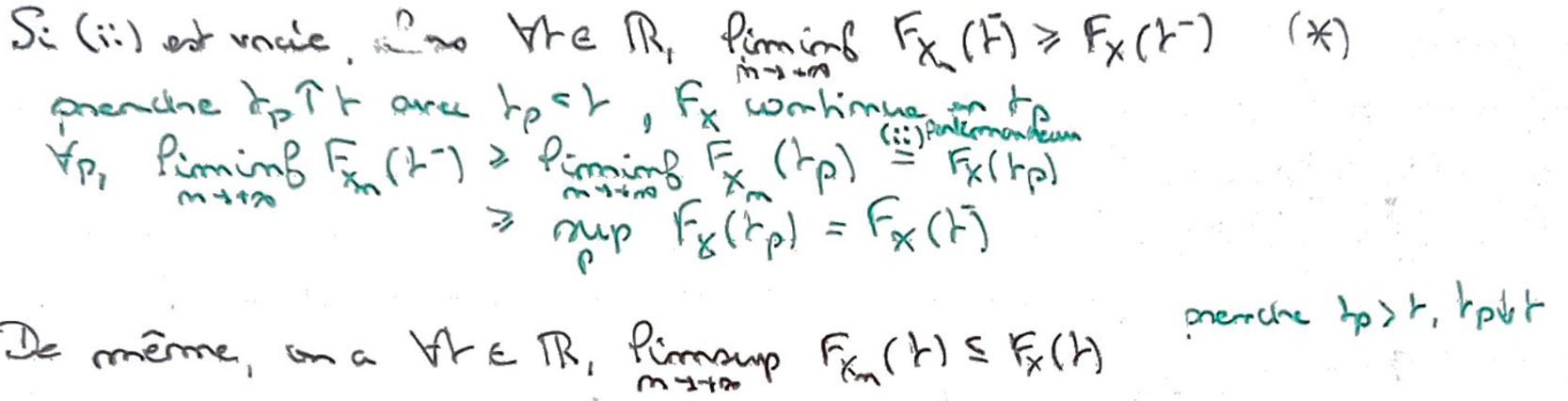
    1i: On a des inégalités avec \(\varliminf\) et \(\varlimsup\) de \(F_{X_n}\) via le Théorème du porte-manteau.
    2:

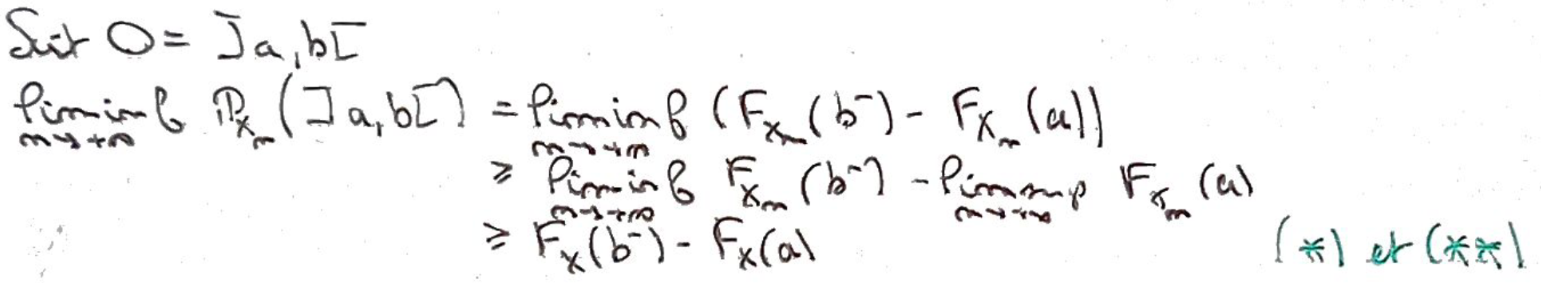
    2i: Si \(O\) est un intervalle de \({\Bbb R}\), alors on peut ainsi minorer \(\varliminf{\Bbb P}_{X_n(]a,b[)}\).
    3:

    3i: Pour un ouvert quelconque de \({\Bbb R}\), on peut faire de même en le décomposant en intervalles ouverts disjoints.
    4:

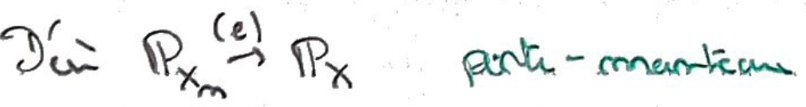
    4i: Cela nous donne la Convergence étroite par Théorème du porte-manteau.
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Traduire le théorème de Lévy pour la Convergence étroite.
    Verso: $$\mu_n\overset{(e)}{\underset{n\to+\infty}\longrightarrow}\mu\quad\iff\quad \forall \xi\in{\Bbb R}^d,\hat\mu_n(\xi){\underset{n\to+\infty}\longrightarrow}\hat \mu(x)$$
    Bonus: (Transformée de Fourier)
    Carte inversée ?:
    END
    Démontrer \((i)\implies(ii)\) :

    \(x\mapsto e^{i\xi x}\) est continue et bornée, donc c'est immédiat.



    Exercices

    Soient \(X_1,X_2,\dots\) des v.a.i.i.d de loi exponentielle \(\mathcal Exp(1)\).
    Montrer que \(\max(X_1,\dots,X_n)-\log n\) converge en loi quand \(n\to+\infty\) et préciser sa limite.

    On va passer par les Fonction de répartitions (qui caractérisent la loi).

    On simplifie par caractère i.i.d..

    Il suffit de vérifier la limite simple de la fonction caractéristique.



    Soient \(X_1,X_2,\dots\) des v.a.i.i.d de loi exponentielle \(\mathcal Exp(1)\).
    Soit \(M_n:=\max(X_1,\dots,X_n)\)

    On va utiliser le Lemme de Borel-Cantelli sur l'événement complémentaire.

    On simplifie la probabilité via le caractère i.i.d. \(\to\) reste à montrer que c'est sommable.

    Réécriture de la puissance via la formule \(a^b=e^{b\ln a}\).

    Un développement limité nous permet de conclure.



    Soient \(X_1,X_2,\dots\) des v.a.i.i.d de loi exponentielle \(\mathcal Exp(1)\).
    Soit \(M_n:=\max(X_1,\dots,X_n)\)

    On va utiliser le Lemme de Borel-Cantelli avec les complémentaires, donc la question revient à montrer la convergence d'une série.

    On développe la probabilité par indépendance.

    On développe la puissance via la formule.

    Développement limité du \(\log\).

    Développement limité de \(\exp\).

    La série converge bien pour \(\varepsilon\) assez petit.


    Soient \(X_1,X_2,\dots\) des v.a.i.i.d de loi exponentielle \(\mathcal Exp(1)\).
    Soit \(M_n:=\max(X_1,\dots,X_n)\)



    Pour généraliser le résultat de la question \(2)\) à tout \(n\), on passe par une majoration et un théorème belge.

    Cela donne bien le résultat voulu.



    Ok en passant par la caractérisation : $$\forall\varphi\in\mathcal C_c({\Bbb R}^d),\quad\int\varphi\,d\mu_n{\underset{n\to+\infty}\longrightarrow}\int\varphi\,d\mu$$ (par composition).


    On va utiliser la caractérisation par les fermés du Théorème du porte-manteau.

    Par continuité de \(f\) \({\Bbb P}_X\)-presque-partout, on a une inclusion avec l'adhérence, qui passe à la \(\limsup\).

    Pour conclure, il nous suffit de montrer que \(\overline{f^{-1}(F)}\subset f^{-1}(F)\), aux points de discontinuité près.

    Ca se fait en prenant une suite de \(f^{-1}(F)\) convergente, et en regardant si sa limite est un point de discontinuité ou non, par disjonction de cas.

    On peut alors majorer la probabilité via cette inclusion, ce qui nous permet de conclure.



    On va montrer la convergence étroite.

    On transforme cette espérance via une série d'indicatrices qui dépendent de la valeur de \(N\).

    On veut montrer qu'on a la convergence simple des espérances.

    On a déjà un résultat qui vient de la convergence en loi de \((X_n)_n\).

    Cela permet de majorer la série, ce qui prouve bien la convergence en loi.


    Faire l'application :

    Pour utiliser le début de l'exercice, il faut montrer que \(N_a\) n'est pas borné lorsque \(a\to+\infty\).

    On peut majorer cette probabilité via l'Inégalité de Markov, puisque la loi de \(N_a\) est connue.

    Si on ne prend pas en compte \(N_a\), on a la convergence en loi via le Théorème central limite.

    Le début de l'exercice nous permet donc de conclure.



  • Rétroliens :
    • Lemme de Slutsky
    • Théorème de convergence de Lévy